Probability and Statistics 2

Chapter 1 Background in Probability

1.2 Random Variables

1. measurable map

   1. Remark of Thm [a sufficient condition for measurable map]

      If \(\mathcal S\) is a \(\sigma\)-field , then \(\{X^{-1}(B)|B\in \mathcal S\}\) is a \(\sigma\)-field

      Def : [generation of measurable map] \(\sigma(X)\) is the \(\sigma\)-field generated by \(X\) \[ \sigma(X)=\{X^{-1}(B)|B\in \mathcal S\} \]

      \(\sigma(X)\) is the smallest \(\sigma\)-field on \(\Omega\) that makes \(X\) a measurable map to \((S,\mathcal S)\) .

   2. Thm [measurable map composition] : If \(X:(\Omega,\mathcal F)\to(S,\mathcal S)\) , \(f:(S,\mathcal S)\to (T,\mathcal T)\) are both measurable maps , then \(f\circ X\) is a measurable map \((\Omega,\mathcal S)\to(T,\mathcal T)\) .

      Proof : \((f\circ X)^{-1}(B)=X^{-1}(f^{-1}(B))\) , \(C:=f^{-1}(B)\in \mathcal S\) , \(X^{-1}(C)\in \mathcal F\)

   3. Cor : If \(X_1,\cdots,X_n\) are random variables , \(f:(\mathbb R^n,\mathcal R^n)\to(\mathbb R,\mathcal R)\) is measurable , then \(f(X_1,\cdots,X_n)\) is a random variable .

   4. (*) Cor : \(X_1,\cdots,X_n\) are random variables , then \(X_1+\cdots+X_n\) is a random variable .

   5. (*) Thm : \(X_1,\cdots\) are random variables , then \(\inf_n X_n\) , \(\sup_n X_n\) , \(\liminf_n X_n\) , \(\limsup_n X_n\) are random variables

      Proof : \(\{\inf_n X_n<a\}=\cup_n\{X_n<a\}\in\mathcal F\) . \[ \liminf_{n\to \infty}X_n=\sup_n\left(\inf_{m\ge n}X_m\right) \] \(Y_n=\inf_{m\ge n}X_m\) is a random variable .

2. (*) Generalization of random variable

   1. Def : [Converges almost surely]

      From Thm above , the following set is a measurable set \[ \Omega_o:=\{w:\lim_{n\to\infty}X_n\text{ exists}\}=\{w:\limsup_{n\to\infty}X_n-\liminf_{n\to\infty}X_n=0\} \] If \(P(\Omega_o)=1\) , then \(X_n\) converges almost surely ( a.s. ) .

      即一列 \(X_n\) 是几乎处处收敛的 当且仅当 \(X_n\) 不收敛的点集测度为 \(0\)

      Def : \(X_\infty:=\limsup_{n\to \infty} X_n\)

      Problem : \(X_{\infty}\) can have value \(\pm\infty\) .

   2. Def : [Generalized random variable]

      A function whose domain is \(D\in \mathcal F\) and range is \(\mathbb R^*:=[-\infty,+\infty]\) is a random variable if \(\forall B\in \mathcal R^* , X^{-1}(B)\in \mathcal F\) .

      Def : [Extended Borel set ] : \(\mathcal R^*\) is generated by intervals of form \([-\infty,a),(a,b),(b,+\infty]\) , \(a,b\in \mathbb R\) .

      extended real line \((\mathbb R^*,\mathcal R^*)\) is a measurable space

1.3 Distribution

1. Definition of Distribution

   1. Def : [distribution] \(X\) is a random variable , then let \(\mu=P\circ X^{-1}\) ( \(\mu(A)=P(X\in A)\) ) , \(\mu\) is a probability measure called distribution .

   2. Check \(\mu\) is a probability measure \((\mathbb R,\mathcal R)\to (\mathbb R,\mathcal R)\) .

      • \(\mu(A)=P(\{w\in \Omega:X(w)\in A\})\ge 0\)

      • If \(A_i\in \mathcal R\) are disjoint countable sequence , then \(X^{-1}(A_i)\) are also disjoint \[ \begin{aligned} \mu(\cup_i A_i)&=P(X^{-1}(\cup_i A_i))\\ &=P(\cup_i X^{-1}(A_i))\\ &=\sum_{i} P(X^{-1}(A_i))\\ &=\sum_{i} \mu(A_i) \end{aligned} \]

2. distribution function

   1. Def : [distribution function] Let \(F(x)=P(X\le x)\) , \(F(x)\) is the distribution function .

      \(F(x)=P(X\le x)\) : Let \(A_x=(-\infty,x]\) , \(F(x)=P(X^{-1}(A_x))=\mu(A_x)\)

      \(F(x)\) can be viewed as the CDF of \(\mu\) / the Stieltjes measure function

   2. Thm [Props of distribution function] : Let \(F\) be a distribution function

      • \(F\) : non-decreasing

      • \(\lim\limits_{x\to -\infty }F(x)=0\) , \(\lim\limits_{x\to+\infty}F(x)=1\)

      \(x\to -\infty , \{X\le x\}\downarrow \varnothing\) , \(x\to+\infty , \{X\le x\}\uparrow \Omega\)

      • \(F\) : right continuous , \(F(x^+)=\lim_{y\downarrow x}F(y)=F(x)\)

      \(y=x+\epsilon\) , \(\{X\le y\}=\{X\le x+\epsilon\}\downarrow \{X\le x\}\)

      • \(F(x^-)=P(X<x)\)

      \(y=x-\epsilon\) , \(\{X\le y\}=\{X\le x-\epsilon\}\uparrow \{X<x\}\)

      • \(P(X=x)=F(x)-F(x^-)\)

   3. Thm [Judgement of distribution function] : \(F\) satisfies (i) , (ii) , (iii) is a distribution function

      Proof : [construction]

      Let \(\Omega=(0,1)\) , \(\mathcal F\) is the corresponding Borel set , \(P\) is Lebesgue measure , so \(P((a,b])=b-a\) .

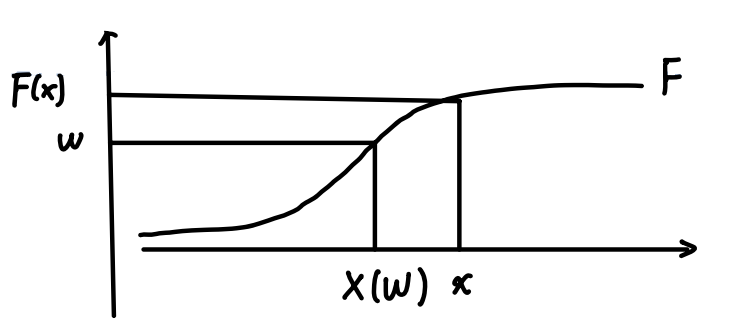
      Let \(X(w)=\sup\{y:F(y)<w\}\) , we want to prove that \(P(X\le x)=F(x)\) .

      Since \(F(x)=P(\{w:w\le F(x)\})\) , we want to prove that : \[ \{w:X(w)\le x\}=\{w:w\le F(x)\} \quad\quad \quad (*) \] \(R\subset L\) : \(\forall w,w\le F(x)\) , and \(X(w)=\sup\{y:F(y)<w\}\) , so \(F(X(w))\le w\le F(x)\) , so \(X(w)\le x\) .

      \(R^c\subset L^c\) : \(\forall w,w>F(x)\) , and \(X(w)=\sup\{y:F(y)<w\}\) .

      \(F\) : right continuous , so \(\exists \epsilon>0\) , \(F(x+\epsilon)<w\) , so \(X(w)\ge x+\epsilon>x\) .

      Equation (*) means :

      

   4. Remark

      Each distribution function \(F\) corresponds to a unique distribution measure \(\mu\)

      One distribution function \(F\) can correspond to many different random variables

      Def [equal in distribution] : If \(X,Y\) have same distribution measure/function , then \(X\) and \(Y\) are equal in distribution , denote as \(X\overset{d}{=}Y\) or \(X=_d Y\) .

3. Density function

   1. Def [density function] : when a distribution function \(F(x)=P(X\le x)\) has the form \[ F(x)=\int_{-\infty}^x f(y)\ dy \] then \(X\) has the density function \(f\) , denote as \(f_X(x)\) .

      \[ P(X=x)=\lim_{\epsilon\to0}\int_{x-\epsilon}^{x+\epsilon} f(y)dy=0 \]

   2. Prop : (necessary and sufficient)

      • \(f(x)\ge 0\)
      • \(\int_{-\infty}^{+\infty}f(x)dx=1\)

4. Discrete / Continuous

   A probability measure \(P\) is discrete if there exists a countable set \(S\) that \(P(S^c)=0\) ( only non-zero on countable set) .

   Discrete : usually \([a_i,b_i)\) segments like .

1.4 Integration

Intuition : Expectation needs Integration .

1. Notations

   1. Def : \((\Omega,\mathcal F)\) , with measure \(\mu\) , \(f:(\Omega,\mathcal F)\to(\mathbb R,\mathcal R)\) . Denote the integration as \(\int fd\mu\) .

   2. Restriction for \(\mu\) : should be \(\sigma\)-finite measure

      e.g. Lebesgue measure is \(\sigma\)-finite : \(A_i=[-i,i]\) , so \(\mu(A_i)<\infty\) and \(\cup_i{A_i}=\mathbb R\) .

   3. Restriction for \(\int fd\mu\) :

      1. \(\varphi\ge 0\) \(\mu\)-a.e. , then \(\int\varphi d\mu\ge 0\)

      Def [almost everywhere] : \(\mu\)-a.e. : \(\mu(\{w:\varphi(w)<0\})=0\) .

      2. \(\int a\varphi d\mu=a\int \varphi d\mu\)

      3. \(\int (\varphi+\psi)d\mu=\int \varphi d\mu+\int \psi d\mu\)

      4. \(\varphi\le \psi\) \(\mu\)-a.e. , then \(\int \varphi d\mu\le \int \psi d\mu\)

      5. \(\varphi=\psi\) \(\mu\)-a.e. , then \(\int \varphi d\mu=\int \psi d\mu\)

      6. \(\left|\int \varphi d\mu\right|\le \int |\varphi|d\mu\)

   4. Thm : (i),(ii),(iii) can derive (iv),(v),(vi)

2. Simple Function

   1. Def [simple function] : If \(\varphi(\omega)=\sum_{i=1}^n a_i \mathbb 1_{A_i}\) , and \(A_i\) are disjoint sets , \(\mu(A_i)<\infty\)

   2. Def [simple function integration] : If \(\varphi(\omega)=\sum_{i=1}^n a_i \mathbb 1_{A_i}\) , define \[ \int \varphi d\mu=\sum_{i=1}^n a_i \mu(A_i) \]

   3. Check Props

      1. : \(\varphi\ge 0\) \(\mu\)-a.e. , so for all \(A_i\) with \(\mu(A_i)>0\) , \(a_i\ge 0\) .

      2. : trivial

      3. : Suppose \(\varphi=\sum_{i=1}^m a_i \mathbb 1_{A_i}\) , \(\psi=\sum_{j=1}^n b_j \mathbb 1_{B_j}\)

      Define \(A_0=\cup_{j} B_j-\cup_i A_i\) , \(B_0=\cup_i A_i-\cup_j B_j\) . Let \(a_0=b_0=0\) .

      Therefore \(\cup_{j=1}^n B_j\subset \cup_{i=0}^n A_i\) and \(\cup_{i=1}^m A_i\subset \cup_{j=1}^n B_j\) . \[ \begin{aligned} \int(\varphi+\psi)d\mu&=\sum_{i=0}^m \sum_{j=0}^n (a_i+b_j)\mu(A_i\cap B_j)\\ &=\sum_{i=0}^m a_i\sum_{j=0}^n \mu(A_i\cap B_j)+\sum_{j=0}^nb_j\sum_{i=0}^m \mu(A_i\cup B_j)\\ &=\sum_{i=0}^m a_i\mu(A_i)+\sum_{j=0}^n b_j\mu(B_j)\\ &=\int \varphi d\mu +\int \psi d\mu \end{aligned} \]