Probability and Statistics 3

Chapter 1 Background in Probability

1.4 Integration

1. Judgement : an integration should satisfies :

   1. \(\varphi\ge 0\) \(\mu\)-a.e. , then \(\int\varphi d\mu\ge 0\)

   2. \(\int a\varphi d\mu=a\int \varphi d\mu\)

   3. \(\int (\varphi+\psi)d\mu=\int \varphi d\mu+\int \psi d\mu\)

2. Basic Properties of integration

   4. \(\varphi\le \psi\) \(\mu\)-a.e. , then \(\int \varphi d\mu\le \int \psi d\mu\)

   5. \(\varphi=\psi\) \(\mu\)-a.e. , then \(\int \varphi d\mu=\int \psi d\mu\)

   6. \(\left|\int \varphi d\mu\right|\le \int |\varphi|d\mu\)

3. Bounded Function

   1. Def [ Bounded Function ] : \(\exists M<\infty,|f(x)|\le M\) , and \(\exists E\subseteq \Omega , \mu(E)<\infty,f(E^c)=0\) .

   2. Def [ Integration for Bounded Function ] : Let \(\Phi_s\) be the set of simple functions . If \(f\) is a bounded function, \[ \int fd\mu:=\sup_{\varphi\in \Phi_s , \varphi\le f}\int \varphi d\mu =\inf_{\psi\in \Phi_s , \psi\ge f}\int \psi d\mu \]

      \(\varphi \le f,\psi\ge f\) : \(\mu\)-a.e.

      Intuition : Like Darboux's upper sum and lower sum

   3. Proof of \(\sup\limits_{\varphi\in \Phi_s , \varphi\le f}\int \varphi d\mu =\inf\limits_{\psi\in \Phi_s , \psi\ge f}\int \psi d\mu\)

      1. By Prop (iv) , \(\varphi\le f\le \psi\) , so \(\int \varphi d\mu\le \int \psi d\mu\)

      2. Prove \(\sup\limits_{\varphi\in \Phi_s , \varphi\le f}\int \varphi d\mu \ge \inf\limits_{\psi\in \Phi_s , \psi\ge f}\int \psi d\mu\)

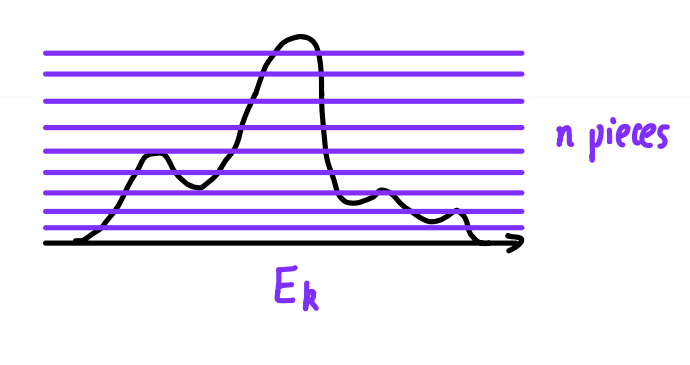
         Since \(|f|\le M\) , let \(E_k:=\{x\in E|\frac{(k-1)M}{n}<f(x)\le \frac{kM}{n}\}\) , \(-n\le k\le n\) .

         Let \(\varphi_n=\sum\limits_{k=-n}^n \frac{(k-1)M}{n}\mathbb 1_{E_k}\) , \(\psi_n=\sum\limits_{k=-n}^n \frac{kM}{n}\mathbb 1_{E_k}\)

         Therefore , \(\int (\psi_n-\varphi_n)d\mu=\frac{M}{n}\mu(E)\) , \[ \sup\limits_{\varphi\in \Phi_s , \varphi\le f}\int \varphi d\mu \ge\int \varphi_nd\mu =-\frac{M}{n}\mu(E)+\int \psi_n d\mu \ge -\frac{M\mu(E)}{n}+\inf\limits_{\psi\in \Phi_s , \psi\ge f}\int \psi d\mu \] When \(n\to +\infty\) , \(-\frac{M\mu(E)}{n}\to 0\) , so \(\sup\limits_{\varphi\in \Phi_s , \varphi\le f}\int \varphi d\mu =\inf\limits_{\psi\in \Phi_s , \psi\ge f}\int \psi d\mu\) .

         

         diagram of the proof

   4. Proof of (i)(ii)(iii)

      1. : Let \(\varphi=0\) , trivial

      2. : For \(a>0\) , \(a\varphi\le af\iff \varphi\le f\) \[ \int afd\mu =\sup_{a\varphi\le af}\int a\varphi d\mu =\sup_{\varphi\le f}\int a\varphi d\mu=a\sup_{\varphi\le f}\int \varphi d\mu=a\int fd\mu \]

      3. : Firstly prove \(\int (f+g)d\mu\le \int fd\mu +\int gd\mu\) .

      Let \(\Phi_s'=\{\psi|\exists \psi_1,\psi_2,\psi=\psi_1+\psi_2,\psi_1\ge f,\psi_2\ge g\}\) , so \(\Phi_s'\subseteq \{\psi|\psi\ge f+g\}\) . \[ \begin{aligned} \int(f+g)d\mu&=\inf_{\psi\ge f+g} \psi d\mu\\ &\le \inf_{\psi=\psi_1+\psi_2\in \Phi_s'} (\psi_1+\psi_2)d\mu\\\ &=\inf_{\psi_1\ge f,\psi_2\ge g} \int \psi_1d\mu+\int \psi_2d\mu\\ &=\inf_{\psi_1\ge f} \int \psi_1d\mu+\inf_{\psi_2\ge g}\int \psi_2d\mu\\ &=\int fd\mu+\int gd\mu \end{aligned} \] Use (ii) , let \(a=-1\) , so \(\int -(f+g)d\mu\le \int (-f)d\mu+\int (-g)d\mu\) , so \(\int (f+g)d\mu\ge \int fd\mu+\int gd\mu\) .

4. Non-Negative Function

   1. Compare with bounded function

      • can exists \(x\) , \(f(x)\to\infty\)
      • the smallest \(E\) s.t. \(f(E^c)=0\) , may be \(\mu(E)\to\infty\)

   2. Notation :

      • \[ \int_E fd\mu:=\int f\cdot \mathbb 1_{E}d\mu \]

      • \[ a\land b:=\min\{a,b\} \]

      • Def [ Integration for non-negative function ] For non-negative function \(f\) , \[ \int fd\mu=\sup\left\{\small\int hd\mu\mid 0\le h\le f,h\text{ bounded function}\right\} \]

        \(h\) is bounded function , so \(\int hd\mu\) is bounded , but \(\sup \int hd\mu\) can be unbounded .

   3. Lemma :

      If \(E_n\uparrow \Omega , \mu(E_n)<\infty\) , then \[ \int_{E_n}f\land nd\mu\uparrow \int fd\mu \]

      This lemma needs \(\mu\) be a \(\sigma\)-finite measure.

      \((f\land n)\cdot \mathbb 1_E\in \{h|0\le h\le f,h\text{ bounded function}\}\)

      Proof

      It's easy to find that \(\lim\limits_{n\to\infty}\int_{E_n}f\land n\ d\mu=\sup\limits_{n\ge 1}\int_{E_n}f\land n\ d\mu\le \int fd\mu\) .

      We only need to prove that \(\forall h,|h|<M,0\le h\le f\) , \(\lim\limits_{n\to\infty}\int_{E_n}f\land n\ d\mu\ge \int fd\mu\) .

      \(\forall n>M\) , \(\int_{E_n} f\land n\ d\mu\ge \int_{E_n}hd\mu=\int hd\mu-\int_{E_n^c}hd\mu\) .

      And \(\int_{E_n^c} hd\mu\le M\mu(E_n^c\cap \{x|h(x)>0\})\) .

      Since \(n\to \infty , \mu(E_n^c\cap \{x|h(x)>0\})\to 0\) \((*)\) .

      Therefore , \(\liminf\limits_{n\to \infty} \int_{E_n} f\land n\ d\mu\ge \int hd\mu\) .

      To prove \((*)\)

      Let \(a_n=\mu(E_n^c\cap \{x|h(x)>0\})\) , we only need to prove that \(\lim_{n\to \infty} a_n=0\) .

      Way 1 : \(a_n\) non-increasing , \(a_n\ge 0\) , so \(\lim_{n\to\infty} a_n=c\)

      If \(c>0\) , then \(\exists \tilde \Omega\subseteq \Omega , \mu(\tilde\Omega)=c\) , \(\forall n,\tilde\Omega\cap E_n=\varnothing\) .

      Therefore , \(\tilde \Omega\cap \bigcup_{n=1}^{\infty}E_n=\varnothing\) , so \(\tilde \Omega\cap\Omega=\varnothing\) , contradicts .

      Way 2 : By definition , \(E_1^c\supset E_2^c \supset\cdots\) , so \(E_n^c=\bigcap_{m=1}^n E_m^c\) .

      \(\lim_{n\to\infty}a_n=\mu(\bigcap_{m=1}^{\infty}E_m^c\cap\{x|h(x)>0\})=\mu(\Omega^c\cap\{x|h(x)>0\})=0\)

   4. Proof of (i)(ii)(iii)

      1. trivial (non-negative)

      2. \(a>0\) , so \(ah\le af\iff h\le f\) \[ \begin{aligned} \int af\ d\mu&=\sup\{\int ah\ d\mu|0\le ah\le af,ah\text{ bounded function}\}\\ &=\sup\{a\int h\ d\mu|0\le h\le f,h\text{ bounded function}\}\\ &=a\int fd\mu \end{aligned} \]

      3. Firstly prove \(\int (f+g)d\mu\ge \int fd\mu+\int gd\mu\)

      Consider bounded function \(k,h\) , \(f\ge h,g\ge k\) , so ,

      \(\int (f+g)d\mu\ge \sup_{0\le h\le f}\int hd\mu+\sup_{0\le k\le g}\int gd\mu=\int fd\mu+\int gd\mu\)

      Secondly prove \(\int(f+g)d\mu\le \int fd\mu+\int gd\mu\)

      Use Lemma , \((f+g)\land n\le (f\land n)+(g\land n)\) .

      Therefore , \(\int_{E_n}(f+g)\land n\ d\mu\le \int_{E_n}f\land n\ d\mu+\int_{E_n} g\land n\ d\mu\) .

      As \(n\to\infty\) , \(\int (f+g)d\mu\le \int fd\mu+\int gd\mu\)

5. General Function

   1. Def [ Integralable ] : \(f\) is integralable if \(\int |f|d\mu<\infty\)

   2. Def [ Integration for General Function ] : If \(f\) is integralable , define

      \(f^+(x):=f(x)\cdot\mathbb 1(f(x)\ge 0)\) , \(f^-(x):=|f(x)|\cdot \mathbb 1(f(x)<0)\)

      Therefore , \(f(x)=f^+(x)-f^-(x)\) , and \(f^+,f^-\) non-negative \[ \int fd\mu:=\int f^+d\mu-\int f^-d\mu \]

      Note : If \(f\) is not integralable , then \(\int f^+d\mu\) , \(\int f^-d\mu\) can both be \(\infty\) , \(\infty-\infty\) not well-defined.

6. Lebesgue Integration

   1. When \(\mu\) is Lebesgue measure : \(\mu((a,b])=b-a\) .

      \(\int fd\mu\) is Lebesgue Integration of \(f\) .

   2. Compare with Riemann Integration

      

      Riemann Integration and Lebesgue Integration

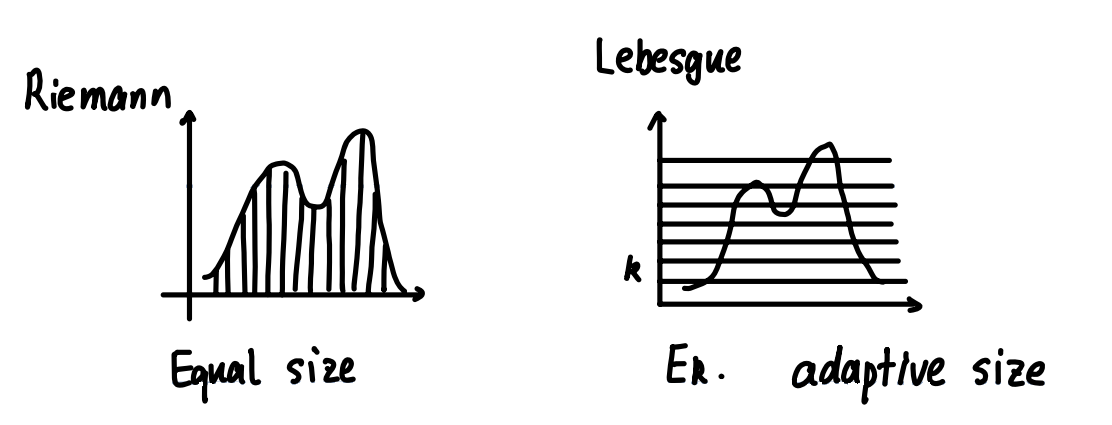
      Lebesgue is more powerful

      E.g. Dirichlet function \(\mathbb 1_{\mathbb Q}\) , \(\int_{[0,1]}\mathbb 1_{\mathbb Q}\)

      • Riemann integration : not integralable , \(\mu(\{x:\mathbb 1_{\mathbb Q}\text{ incontinuous at }x\})>0\)
      • Lebesgue integration : integralable : \(\int_{[0,1]}\mathbb 1_{\mathbb Q}=\mu(\mathbb Q\cap [0,1])=0\)

7. Formal Definition of PDF

   1. Def [ Absolutely Continuous ] : \(\nu\) is absolutely continuous w.r.t \(\mu\) ( denote as \(\nu\ll \mu\) ) if

      \(\forall A\in \mathcal F\) , \(\mu(A)=0\Rightarrow \nu(A)=0\)

   2. Thm [ Radon-Nikodym ] : measurable space \((\Omega,\mathcal F)\) with \(\sigma\)-finite measure \(\nu,\mu\) , \(\nu\ll\mu\)

      Then \(\exists g\ge 0,\forall E\in \mathcal F,\int_Egd\mu=\nu(E)\)

      \(g\) is called Radon-Nikodym derivative

   3. Prop : If \(\exists g,h\) , \(\int_Egd\mu=\int_Ehd\mu=\nu(E)\) , then \(g\equiv h\) a.e.

   4. Def [ PDF ] : When \(\nu\) is a distribution measure , \(\mu\) is Lebesgue measure , \(g\) is the probability density function for \(\nu\) .

      Observation : \(\nu(E)=P(X\in E)=\int gd\mu\)

   5. Prop : \(g\) is \(\mathcal F\)-measurable , i.e. \(g\) is a measurable map \((\Omega,\mathcal F)\to(\mathbb R,\mathcal R)\) .

1.5 Properties of Integration

1. Jenson's Inequality

   1. Def [ convex ] : \(\varphi\) is a convex , if \(\forall \lambda\in (0,1) , \lambda\varphi(x)+(1-\lambda)\varphi(y)\ge \varphi(\lambda x+(1-\lambda)y)\)

   2. THM [ Jenson's Inequality ] : If \(\varphi\) is a convex , \(\varphi\circ f\) is integralable , \(\mu\) is a probability measure , \[ \varphi\left(\int fd\mu\right)\le \int (\varphi \circ f)d\mu \]

   3. Proof :

      For convex \(\varphi\) , we can find a line \(L(x)=ax+b\) , s.t. \(\varphi(x)\ge ax+b\) , and equal iff \(x=\int fd\mu\) . \[ \begin{aligned} \int (\varphi \circ f)d\mu&\ge \int (ax+b)\circ fd\mu\\ &=a\int fd\mu+\int bd\mu\\ &=a\int fd\mu+b\mu(\Omega)\\ &=a\int fd\mu+b\\ &=L\left(\int fd\mu\right)\\ &=\varphi\left(\int fd\mu\right) \end{aligned} \]