Algorithm Design 6

Chapter 4 NP Completeness

4.4 Other Problems in NPC

Intuition : Find problems \(L\in NP\) that \(SAT\le_p L\) .

4.4.1 3-SAT

1. Description :

   1. Def [ literal ] : For \(\vec x=(x_1,\cdots,x_n)\in \{0,1\}^n\) , literal is an element of \(X=\{x_i|i\in [n]\}\cup\{\bar x_i|i\in [n]\}\) .

      Def [ CNF-clause ] : A CNF-clause \(c\) is a formula with form : \[ c=\lor_{j=1}^m a_j \] where \(a_1,\cdots,a_m\) are distinct literals .

      Def [ CNF ] : A conjunctive normal formula (CNF) is a formula \(\{0,1\}^n\to \{0,1\}\) with following form : \[ f(\vec x)=\land_{i=1}^k c_i(\vec x) \] where \(c_i(\vec x)\) is a CNF-clause .

      Def [ 3-CNF ] : A 3-CNF is a CNF with all clauses having exactly \(3\) literals . \(c_i=a_{i,1}\lor a_{i,2}\lor a_{i,3}\) , where \(a_{i,1},a_{i,2},a_{i,3}\) are distinct literals .

   2. Input : a 3-CNF

      Output : Decide whether there exists an assignment for \(\vec x\) such that \(f(\vec x)=1\) .

2. 3-SAT is NPC

   Obviously , 3-SAT is NP .

   Goal : SAT $_p $ 3-SAT

   Given a SAT instance \(I\) , we construct in poly-time a 3-SAT instance \(I'\) , s.t. \(I\in SAT\iff I'\in 3-SAT\) .

   Cook reduction : can use oracle poly times
   Karp reduction : only use oracle once

   Originally , Cook define NPC by Cook reduction , but almost always Karp reduction is enough (though stronger than Cook's) ,

   For each node \(v\in I\) , construct a variable \(x_v\) in \(I'\)

   • If \(v=\lnot\) with child \(u\) , we need \(x_v=\overline{x_u}\) , so add to \(I'\) a clause \((x_v\lor x_u)\land (\overline{x_v}\lor\overline{x_u})\) .
   • If \(v=\lor\) with children \(u,w\) , we need \(x_v=x_u\lor x_w\) , so add to \(I'\) a clause \((x_v\lor \bar x_u)\land (x_v\lor \bar x_w)\land (\bar x_v\lor x_u\lor x_w)\) .
   • If \(v=\land\) with children \(u,v\) , we need \(x_v=x_u\land x_w\) , so add to \(I'\) a clause \((\bar x_v\lor x_u)\land (\bar x_v\lor x_w)\land (x_v\lor \bar x_u\lor \bar x_w)\) .
   • If \(v=0/1\) , add to \(I'\) a clause \(\bar x_v\) or \(x_v\) .

   Extend each clause into \(3\) literals : \((a\lor b)=(a\lor b\lor c)\land (a\lor b\lor \bar c)\)

   Claim : \(I\in SAT\iff I'\in 3-SAT\)

4.4.2 Independent Set ( IS )

Obviously , IS is NP

Goal : 3-SAT \(\le_p\) IS

1. Construction

   Given 3-SAT instance \(I\) , construct an IS instance \(I'=(G,k)\) , s.t. \((G,k)\in\) IS $I$ 3-SAT .

   • Each clause \(x_{i,1}\lor x_{i,2}\lor \bar x_{i,3}\) , construct a 3-cycle \((x_{i,1} , x_{i,2} , \bar x_{i,3})\) (finally \(3n\) nodes , \(3n\) edges).
   • Then connecting \(x_i\) and \(\bar x_i\) for all \(i\) .

   In each triangle , we can choose at most \(1\) node .

2. Claim : \((G,k)\in\) IS $I$ 3-SAT ( \(k\) is the number of clauses )

   Proof :

   1. If $I$ 3-SAT , then there is a valid assignment \(\vec x\) . Each clause has at least one true , so we choose that literal in the clause , this is an independent set in \(G\) with size \(k\) .
   2. If $(G,k)$ IS , for each literal \(x_i\) (\(\bar x_i\)) chosen , let \(x_i=1\) ( \(x_i=0\) ) . The rest of variables are assigned arbitrarily . This assignment is a valid assignment for \(I\) , so \(I\in\) 3-SAT .

3. Cor : Vertex Coloring , Set Coloring \(\in\) NPC

4.4.3 Hamiltonian Cycle ( HC )

1. Description

   1. Input : A directed/undirected graph
   2. Output : Decide whether there exists a cycle visiting each vertex exactly once

   TSP : weighted , determine the shortest Hamiltonian Cycle

   TSP is NP-Hard

2. HC is NPC

   Obviously , HC is NP

   Goal : 3-SAT \(\le_p\) HC

   1. Construction

      Consider an instance \(I\) for 3-SAT , construct \(G\) , s.t. \(G\in\) HC $I$ 3-SAT .

      Suppose \(I\) has \(n\) variables , \(k\) clauses .

      • \(S,T\in V\) , \((T,S)\in E\)

      • \(n\) lines (\(P_i\)) : on line \(i\) : \(x_{i,0/1}\in V\) , \(v_{i,j,0/1/2}\in V\) , \(1\le j\le k\) , \((v_{i,j,0},v_{i,j,1}),(v_{i,j,1},v_{i,j,2}),(v_{i,j,2},v_{i,j+1,0})\in E\)

        \((x_{i,0},v_{i,1,0}) , (v_{i,k,2},x_{i,1})\in E\)

      • Between two lines : \((x_{i,0},x_{i+1,0}) , (x_{i,0},x_{i+1},1) , (x_{i,1},x_{i+1,0}),(x_{i,1},x_{i+1,1})\in E\)

        \((S,x_{1,0}),(S,x_{1,1}),(x_{n,0},T),(x_{n,1},T)\in E\)

      • Clause : For example \(c_a=(x_i\lor \bar x_j\lor x_k)\)

        \(c_a\in V\) , \((v_{i,a,0},c_a),(c_a,v_{i,a,1})\in E\) , \((v_{j,a,1},c_a),(c_a,v_{j,a,0})\in E\) , \((v_{k,a,0},c_a),(c_a,v_{k,a,1})\in E\)

      

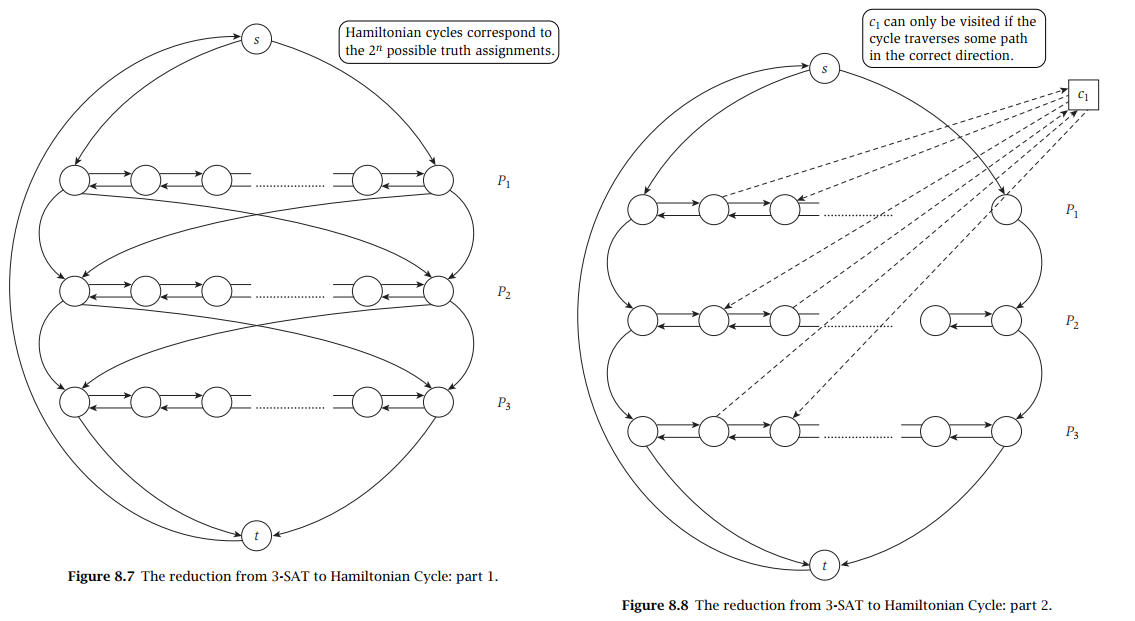
      \(v_{i,j,2}\) for constraining the Hamiltonian cycle be the form \(S\to x_{1,0/1}\to x_{1,1/0}\to \cdots\to x_{n,0/1}\to x_{n,1/0}\to T\to S\) .

   2. Cor : Hamiltonian Cycle / Hamiltonian Path for directed/undirected graph are all NPC .

4.4.4 3-Dimensional Matching ( 3DM)

1. Description

   Def [ 3D graph ] : \(G=(X,Y,Z,E)\) , \(E=\{e=(x_e,y_e,z_e)|x_e\in X,y_e\in Y,z_e\in Z\}\) .

   Def [ 3D Matching ] : \(M\subseteq E\) satisfies

   • $e_1e_2M $, \(x_{e_1}\neq x_{e_2}\) , \(y_{e_1}\neq y_{e_2}\) , \(z_{e_1}\neq z_{e_2}\)
   • \(\bigcup\limits_{e\in M}x_e=X\) , \(\bigcup\limits_{e\in M}y_e=Y\) , \(\bigcup\limits_{e\in M}z_e=Z\).

   Input : A 3D graph

   Output : Decide whether there is a 3D Matching for this graph.

2. 3DM is NPC

   Obviously , 3DM is NP

   Goal : 3-SAT \(\le_p\) 3DM

   Consider an instance \(I\) for 3-SAT , construct \(G\) , s.t. \(G\in\) 3DM $I$ 3-SAT .

   Suppose \(I\) has \(n\) variables , \(k\) clauses .

   Construction :

   Vertices :

   • For each variable \(x_i\) , construct \(A_i=\{a_{i,1},\cdots,a_{i,2k}\}\) , \(B_i=\{b_{i,1},\cdots,b_{i,k}\}\) , \(C_i=\{c_{i,1},\cdots,c_{i,k}\}\) .
   • For each clause \(c_i\) , construct \(d_i,e_i\) .
   • Cleanup garget : for \(i\)-th garget construct \(y_i,z_i\) .

   \(X=\bigcup A_i\) , \(Y=\left(\bigcup B_i \right)\cup \{d_i\}\cup\{y_i\}\) , \(Z=\left(\bigcup C_i \right)\cup \{e_i\}\cup\{z_i\}\)

   Hyperedges :

   • For each variable \(x_i\) : \(e_{i,2j-1}=(a_{i,2j-1},b_{i,j},c_{i,j})\) , \(e_{i,2j}=(a_{i,2j},b_{i,j+1},c_{i,j})\) . (\(1\le j\le k\) )
   • For each clause \(c_t\) : suppose \(c_t=x_i\lor \bar x_j\lor x_k\) : \(e_{t,1}=(a_{i,2t},d_t,e_t)\) , \(e_{t,2}=(a_{j,2t-1},d_t,e_t)\) , \(e_{t,3}=(a_{k,2t},d_t,e_t)\) . (\(1\le t\le k\))
   • For each cleanup garget \(g_t\) : \(e_{t,i,j}=(a_{i,j},y_t,z_t)\) . (\(1\le i\le n,1\le j\le 2k\))

   

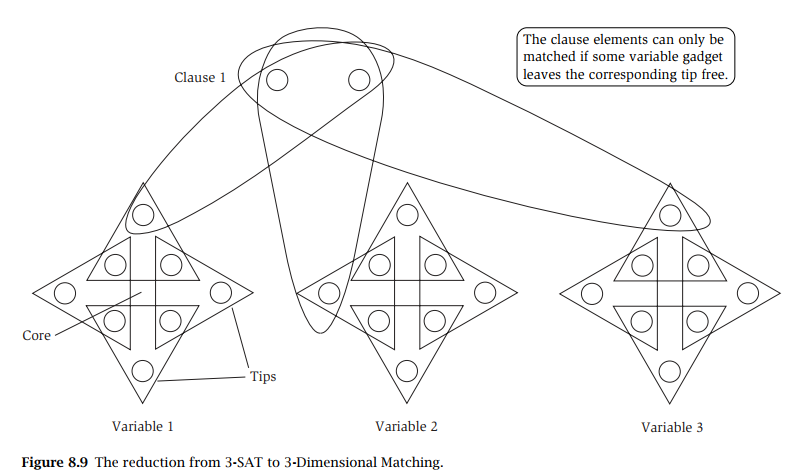
   Cleanup garget : we need \((n-1)k\) gargets to recycle all free \(a_{i,j}\) ( tips ) .

4.4.5 3-Coloring Problem (3CoL)

1. Description

   1. Def [ valid coloring ] : Assign each vertex a color , such that no two vertices having same color share an edge

      \(\forall e=(u,v)\in E\) , \(c(u)\neq c(v)\) .

   2. Def [ chromatic number ] \(\chi(G)\) :The minimum number of colors that can color the graph validly .

   3. Input : A graph \(G\)

      Output : Decide whether \(\chi(G)\le 3\).

   • 2CoL is P , using dfs

   • 4CoL Theorem : Any planar graph can be \(4\)-colored.

     Current Proof : need computer assistant ( \(\sim 10^2\) cases to verify )

     Open : a proof of 4CoL Theorem without computer assistant ?

2. 3CoL is NPC

   Obviously 3CoL is NP .

   Goal : 3CoL \(\le_p\) 3-SAT .

   Consider an instance \(I\) for 3-SAT , construct \(G\) , s.t. \(G\in\) 3CoL $I$ 3-SAT .

   Suppose \(I\) has \(n\) variables , \(k\) clauses .

   Construction :

   Vertices :

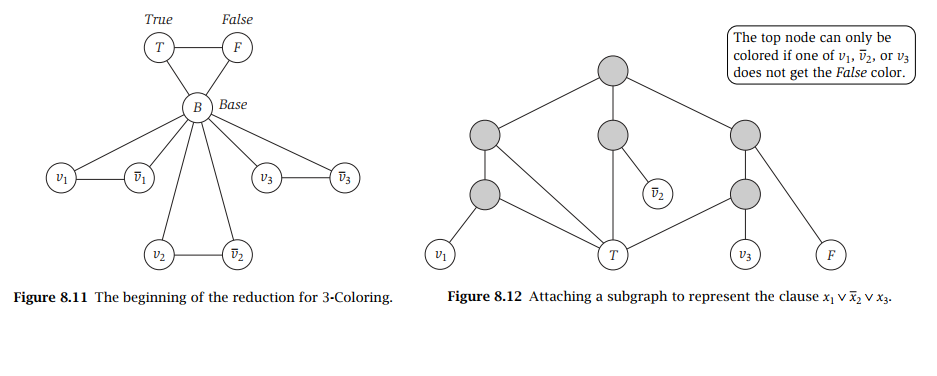
   • Special garget : \(T,F,B\) .
   • Variable garget : \(v_i\) , \(\bar v_i\) .
   • Clause garget : \(6\) vertices for each clause .

   Edges :

   • Special garget : \((T,F),(T,B),(F,B)\)

     To ensure \(T,F,B\) having distinct colors

   • Variable garget : \((B,v_i)\) , \((v_i,\bar v_i)\) , \((B,\bar v_i)\)

     To ensure either \(c(v_i)=c(T),c(\bar v_i)=c(F)\) , or \(c(v_i)=c(F),c(\bar v_i)=c(T)\)

   • Clause garget : Example \(c=(x_i\lor \bar x_j\lor x_k)\)

     \((v_i,a),(T,a),(a,b),(T,b)\)

     \((\bar v_j,c),(T,c)\)

     \((v_k,d),(T,d),(d,e),(F,e)\)

     \((f,a),(f,c),(f,e)\)

     To ensure that \(f\) can be colored if and only if \(v_i,\bar v_j,v_k\) are not all colored with \(c(F)\).

     Otherwise , \(c(v_i)=c(F)\) , so \(c(a)=c(B)\) , so \(c(b)=c(F)\)

     \(c(\bar v_j)=c(F)\) , so \(c(c)=c(B)\)

     \(c(v_3)=c(F)\) , so \(c(d)=c(B)\) , so \(c(e)=c(T)\)

     Then \(f\) cannot be colored

   

4.4.6 Subset Sum Problem

1. Description

   Input : \(w_1,\cdots,w_n\) , target \(W\) .

   Output : determine whether there exists \(S\subseteq [n]\) , s.t. \(\sum_{i\in S}w_i=W\) .

   Subset Sum can be solved in \(\mathcal O(nW)\) with DP method

2. Subset Sum is NPC

   Obviously Subset Sum is NP.

   \(W\) in the reduction must be exponentially large

   Goal : 3DM \(\le_p\) Subset Sum

   1. Construction

      For each hyperedge \(e=(x,y,z)\) , construct \(w_e=2^{x-1+|Y|+|Z|}+2^{y-1+|Z|}+2^{z-1}\)

      Let \(W=\sum\limits_{x=1}^{|X|}2^{x-1+|Y|+|Z|}+\sum\limits_{y=1}^{|Y|}2^{y-1+|Z|}+\sum\limits_{z=1}^{|Z|}2^{z-1}\)

      Problem : carry ( 进位 )

   2. Improved Construction

      Let \(b=|E|+1\)

      For each hyperedge \(e=(x,y,z)\) , construct \(w_e=b^{x-1+|Y|+|Z|}+b^{y-1+|Z|}+b^{z-1}\)

      Let \(W=\sum\limits_{x=1}^{|X|}b^{x-1+|Y|+|Z|}+\sum\limits_{y=1}^{|Y|}b^{y-1+|Z|}+\sum\limits_{z=1}^{|Z|}b^{z-1}\)