Algorithm Design 9
Chapter 7 Divide and Conquer
7.1 Merge Sort & #inversions
Merge Sort
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27// Initial : array a[1,...,n]
function sort(s.t){ // sort a[s,...,t]
if(s>=t) return a[s,...,t];
mid=(s+t)/2;
list1=sort(s,mid);
list2=sort(mid+1,t);
list=merge(list1,list2);
return list;
}
function merge(list1,list2){ // merge two sorted sequence into a sorted sequence
list=[];
while(!list1.empty()&&!list2.empty()){
a=list1.front();
b=list2.front();
if(a<b){
list.push_back(a);
list1.pop_front();
}
else{
list.push_back(b);
list2.pop_front();
}
}
if(!list1.empty())list.append_back(list1);
if(!list2.empty())list.append_back(list2);
return list;
}Time analysis
\(T(n)\) : time to sort \(n\) elements .
\(T(n)=2T(\frac{n}{2})+cn\)
Method 1 : unrolling
Draw the recursive tree
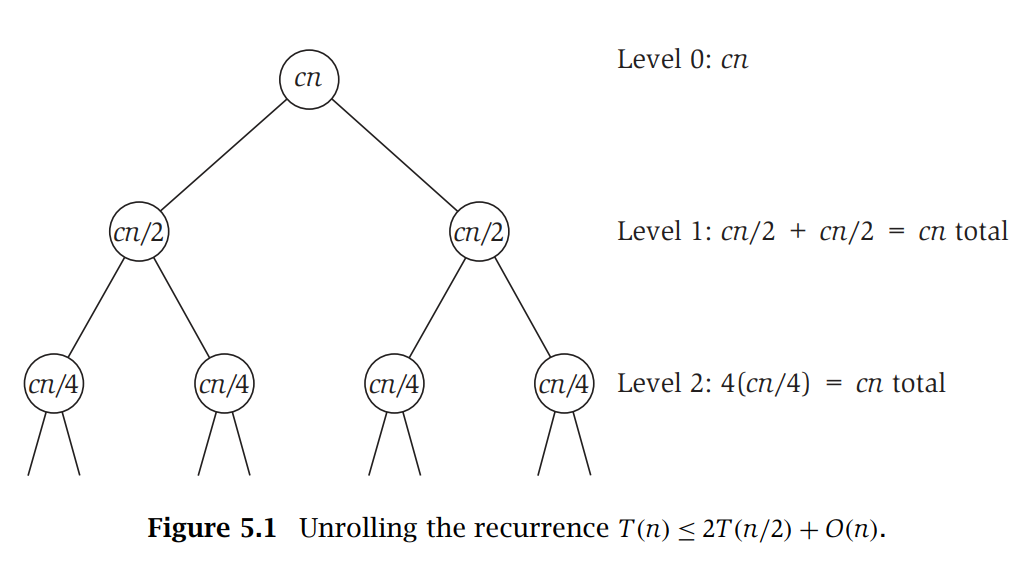
Method 2 : substitution
Guess : \(T(n)\le cn\log_2 n\)
Inductive Proof : \[ \begin{aligned} T(n)&\le 2T(\frac{n}{2})+cn\\ &\le 2c\frac{n}{2}\log_2(\frac{n}{2})+cn\\ &=cn\log_2n-cn+cn\\ &=cn\log_2n \end{aligned} \]
Note : we need to consider precise coefficient here .
Wrong Proof : \(T(n)=O(n)\) \[ T(n)=2T(\frac{n}{2})+O(n)=2O(\frac{n}{2})+O(n)=O(n) \] Approximate constant for \(\log_2 n\) times .
Method 3 : Master Theorem \[ T(n)=\begin{cases} \Theta (1)&n\le n_0\\ aT(\frac{n}{b})+f(n)&n>n_0 \end{cases} \] We can solve \(T(n)\) \[ c_{crit}=\log_{b}a \]
\[ T(n)=\begin{cases} \Theta(n^{c_{crit}})&f(n)=\mathcal O(n^c),c<c_{crit}\\ \Theta(n^{c_{crit}}\log^{k+1}n)&f(n)=\Theta(n^{c_{crit}}\log^k n),k\ge 0\\ \Theta(f(n))&f(n)=\Omega(n^c),c>c_{crit} \end{cases} \]
7.2 Counting inversions
#inversion
Given \(a_1,\cdots,a_n\) , count number of pairs \((i,j)\) s.t. \(i<j\) and \(a_i>a_j\)
View : matching sorted sequence and original sequence , #crossings
counting inversion based on merge sort
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29// Initial : array a[1,...,n]
function sort(s.t){ // sort a[s,...,t]
if(s>=t) return a[s,...,t];
mid=(s+t)/2;
(list1,n1)=sort(s,mid); // inversions only in left part
(list2,n2)=sort(mid+1,t); // inversions only in right part
(list,n3)=merge(list1,list2); // inversions between two parts
return (list,n1+n2+n3);
}
function merge(list1,list2){
// we only count a\in list1 , b\in list2 , a>b
list=[]; n3=0;
while(!list1.empty()&&!list2.empty()){
a=list1.front();
b=list2.front();
if(a<=b){
list.push_back(a);
list1.pop_front();
}
else{
list.push_back(b);
list2.pop_front();
n3+=list1.size(); // for each b , count all valid a
}
}
if(!list1.empty())list.append_back(list1);
if(!list2.empty())list.append_back(list2);
return list;
}
7.3 Find the Closest pair of points in \(\mathbb R^2\)
Current
- naive : \(\mathcal O(n^2)\)
- deterministic : \(\mathcal O(n\log n)\) [Shamos & Hoey]
- randomized : \(\mathcal O(n)\) (with Hash)
D&C Algorithm
- sort all points according to \(x\)-coordinate , divide into Left side and Right side , each with \(\frac{n}{2}\) points
- solve each part
- merge the two parts , compute pairs with one point in Left and the other in Right
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23function solve(s,t){
if(s>=t) return +inf;
int mid=(s+t)/2;
dl=solve(s,mid);
dr=solve(mid+1,t);
d=merge(s,t,min(dl,dr));
return d;
}
functino merge(s,t,delta){
// divide R^2 plane with (delta/2)*(delta/2) grids
// observation : at most 1 point in one grid
// we only need to consider 3 rows upper and 3 rows lower
// columns : 2 columns left and 2 columns right
int d=delta;
list=sort_y(s,t);
list.filter(a:halfline-delta<=a.x<=halfline+delta)
for(int i=0;i<list.size();i++){
for(int j=max(0,i-12);j<=min(list.size()-1,i+12);j++){
d=min(d,dist(a[i],a[j]));
}
}
return d;
}Note : we can firstly sort the points according to \(x\)-coordinate , then within solving and merging , we sort the points according to \(y\)-coordinate . (instead of using a \(\mathcal O(n\log n)\) sorting in
list=sort_y(s,t)) . The total time can be \(\mathcal O(n\log n)\) .
7.4 \(k\)-th smallest number
Description
Given a sequence \(a[1,\cdots,n]\) , find the \(k\)-th smallest number
D&C Algorithm
[Blum , Floyd , Pratt , Rivest , Tarjan 1973]
deterministic , \(\mathcal O(n)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15function Pick(A,k){
x=GenBaseline(A,k);
listl=A.filter(a<x);
listr=A.filter(a>x);
numx=A.count(a==x);
if(k<=listl.size()) return Pick(listl,k);
if(k>listl.size()&&k<=listl.size()+numx) return x;
if(k>listl.size()+numx) return Pick(list2,k-listl.size()-numx);
}
function GenBaseline(A,k){
Divide n elements into n/5 groups
sort each group
listm=all group median
return Pick(listm,n/10);
}Observation : \(\max\{|listl|,|listr|\}\le \frac{7}{10}n\)
If we sort the \(\frac{n}{5}\) groups according to the median , let \(x\) be the median of the medians of the groups .
Then \(x\) is larger than the previous \(\frac{n}{10}\) groups' first \(3\) elements , so \(|listr|\le \frac{7}{10}n\)
And \(x\) is smaller than the later \(\frac{n}{10}\) groups' last \(3\) elements , so \(|listl|\le \frac{7}{10}n\)
\[ T(n)\le cn+T(\frac{n}{5})+T(\frac{7}{10}n) \]
Key : \(\frac{1}{5}+\frac{7}{10}<1\)
7.5 Fast Fourier Transform
Convolution
Sequence \(a[0,\cdots,n-1],b[0,\cdots,m-1]\) .
\((a*b)_k=\sum_{i+j=k}a_ib_j\)
Applications
polynomial multiplication \[ \begin{aligned} A(x)&=\sum_{i=0}^{n-1} a_i x^i\\ B(x)&=\sum_{j=0}^{m-1} b_j x^j\\ C(x)=A(x)B(x)&=\sum_{k=0}^{n+m-2}c_kx^k\\ &=\sum_{k=0}^{n+m-2}\sum_{i+j=k}a_ib_jx^k \end{aligned} \]
signal processing
time \(\to\) frequency
- remove high-frequency \(\to\) remove noise
- multiplication in frequency \(\leftrightarrow\) convolution in time
- filter : smoothing , denoising
sum of two independent r.v.
\(X\) : PDF \(f\) , \(Y\) : PDF \(g\) , \(X+Y\) : PDF \(h\) \[ h(z)=\int_{-\infty}^{\infty} f(x)g(z-x)dx \]
Algorithm (poly multiplication)
- Choose \(n+m-1\) values \(x_1,\cdots,x_{n+m-1}\) , evaluate \(A(x_i),B(x_i)\) (DFT , \(\mathcal O(n\log n)\))
- Let \(C(x_i)=A(x_i)B(x_i)\) (\(\mathcal O(n)\))
- Interpolation , reconstruct \(C(x)\) from \(C(x_i)\) (IDFT , \(\mathcal O(n\log n)\))
DFT
\(\{x_0,\cdots,x_{N-1}\}\to \{\bar x_0,\cdots,\bar x_{N-1}\}\) , where \(N=2^t\) for some positive integer \(t\) . \[ \bar x_k=\sum_{n=0}^{N-1}x_n\exp(-\frac{2\pi \mathrm{i}kn}{N}) \] \(\bar x_k\) can be viewed as \(f(\exp(-\frac{2\pi \mathrm{i}k}{N}))\) .
Denote \(w_k^j=\exp(\frac{2\pi \mathrm{i}j}{k})\) : \(j\)-th root of \(x^k=1\) .
Divide and Conquer for DFT \[ \begin{aligned} A_{even}(x)&=a_0+a_2x+a_4x^2+\cdots+a_{N-2}x^{\frac{N-2}{2}}\\ A_{odd}(x)&=a_1+a_3x+a_5x^2+\cdots+a_{N-1}x^{\frac{N-2}{2}}\\ A(x)&=A_{even}(x^2)+xA_{odd}(x^2) \end{aligned} \] Goal : compute \(A(w_{2N}^0),A(w_{2N}^1),\cdots A(w_{2N}^{2N-1})\) .
Divide : \(A_{even}(w_{N}^0),A_{even}(w_N^1),\cdots,A_{even}(w_N^{N-1})\) , \(A_{odd}(w_N^0) , A_{odd}(w_N^1) , \cdots,A_{odd}(w_N^{N-1})\)
Merge : \(A(w_{2N}^k)=A_{even}(w_N^k)+w_{2N}^k A_{odd}(w_N^k)\) , \(A(w_{2N}^{N+k})=A_{even}(w_N^k)-w_{2N}^{k}A_{odd}(w_N^k)\) , for \(0\le k\le N-1\) .
IDFT \[ \begin{pmatrix} (w_{N}^{0})^0&(w_{N}^{0})^1&\cdots &(w_{N}^{0})^{N-1}\\ (w_{N}^{1})^0&(w_{N}^{1})^1&\cdots &(w_{N}^{1})^{N-1}\\ \vdots&\vdots&\ddots&\vdots\\ (w_{N}^{N-1})^0&(w_{N}^{N-1})^1&\cdots &(w_{N}^{N-1})^{N-1} \end{pmatrix}\begin{pmatrix}a_0\\a_1\\\vdots\\a_{N-1} \end{pmatrix}=\begin{pmatrix}A(w_{N}^0)\\A(w_{N}^1)\\\vdots\\A(w_{N}^{N-1}) \end{pmatrix} \]
\[ W=\begin{pmatrix} (w_{N}^{0})^0&(w_{N}^{0})^1&\cdots &(w_{N}^{0})^{N-1}\\ (w_{N}^{1})^0&(w_{N}^{1})^1&\cdots &(w_{N}^{1})^{N-1}\\ \vdots&\vdots&\ddots&\vdots\\ (w_{N}^{N-1})^0&(w_{N}^{N-1})^1&\cdots &(w_{N}^{N-1})^{N-1} \end{pmatrix} \]
Orthogonal basis : \(WW^\dagger=NI\) , so \(W^{-1}=\frac{1}{N}W^\dagger\) , therefore , \[ \frac{1}{N}\begin{pmatrix} \overline{(w_{N}^{0})^0}&\overline{(w_{N}^{0})^1}&\cdots &\overline{(w_{N}^{0})^{N-1}}\\ \overline{(w_{N}^{1})^0}&\overline{(w_{N}^{1})^1}&\cdots &\overline{(w_{N}^{1})^{N-1}}\\ \vdots&\vdots&\ddots&\vdots\\ \overline{(w_{N}^{N-1})^0}&\overline{(w_{N}^{N-1})^1}&\cdots &\overline{(w_{N}^{N-1})^{N-1}} \end{pmatrix}\begin{pmatrix}A(w_{N}^0)\\A(w_{N}^1)\\\vdots\\A(w_{N}^{N-1}) \end{pmatrix}=\begin{pmatrix}a_0\\a_1\\\vdots\\a_{N-1} \end{pmatrix} \]